delay function is frequently needed in system dynamics for modeling postponed effects, i.e. situations when it takes some time for decision-making, or for some processes to occur before the action is taken. For example, in the classic Bass Diffusion model, delay function is used to model discard rate. In this model people move back from the adopter population to the pool of potential adopters when the product they have purchased is discarded or consumed. So, the discard flow is nothing else but the adoption flow delayed on the average life time of the product.
The plot on the figure below illustrates how the delay function works:
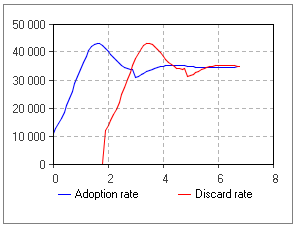
This function can be called in formulas of system dynamics variables and has two notations:
-
delay(flow, delayTime, initialValue)
The function delays the flow specified as the function’s first argument on the specified delay time.
flow can be a flow variable, or a numeric expression of any complexity.
delayTime can be either a constant or a numeric expression (e.g. a function call, or a numeric parameter). The delay function with zero or negative delay time returns the original flow.
Until delayTime is reached, the function will return the initialValue.
-
delay(input, delayTime)
A simplified notation of the function. It is used when the initialValue is zero.
In the example described above, the formula for the DiscardRate will be as follows:
delay(AdoptionRate, ProductLifeTime)
input — unit
delayTime — time
initialValue — unit
delay() — unit
The output units are the same as the input ones.
-
How can we improve this article?
-

