Combining modeling methods

System dynamics -> discrete elements
Discrete elements -> system dynamics
Agent based <-> discrete event

In this section we will consider the techniques of linking different modeling methods in AnyLogic.

The very first thing you should know is that all model elements of all methods, be they SD variables, statechart states, process blocks, and even animation shapes or business charts exist in the “same namespace”: any element is accessible from any other element by name (and, sometimes, “path” — the prefix describing the location of the element).

The following examples are all taken from the real projects and purged of all unnecessary details. This set, of course, does not cover everything, but it does give a good overview of how you can build interfaces between different methods.

System dynamics -> discrete elements

The system dynamics model is a set of continuously changing variables. All other elements in the model work in discrete time (all changes are associated with events). SD itself does not generate any events, so it cannot actively make an impact on agents, process flowcharts, or other discrete time constructs. The only way for the SD part of the model to affect a discrete element is to let that element watch a condition over SD variables, or to use SD variables when making a decision.

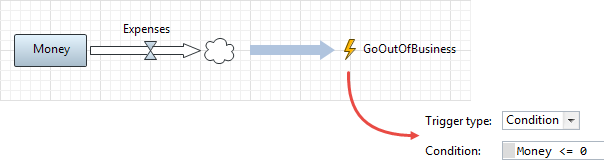
A and B. SD triggers an event or a statechart transition

Events (low-level constructs that allow scheduling a one-time or recurrent action) and statechart transitions are frequent elements of agent behavior. Among other types of triggers, both can be triggered by a condition — a Boolean expression.

If the model contains dynamic variables, all conditions of events and statechart transitions are evaluated at each integration step, which ensures that the event or transition will occur exactly when the (continuously changing) condition becomes true.

The event and the statechart can be located on the same level as the SD, or in a different agent.

A. SD triggers an event

The discrete elements are waiting for the Money stock to fall below zero:

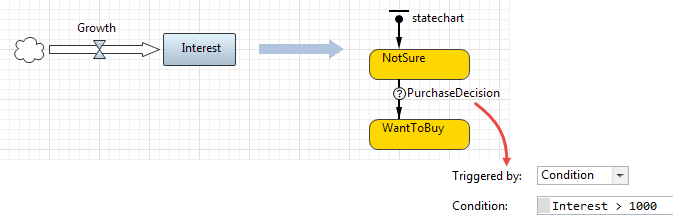
B. SD triggers a statechart transition

The discrete elements are waiting for the Interest to rise higher than a given threshold value:

C. SD controls the event rate

There is an event with a rate trigger type (the time between subsequent occurrences is exponentially distributed). The event rate is set to the dynamic variable, and each subsequent occurrence is scheduled according to the current value of the variable.

D. SD controls the Source arrival rate

The NewPatientAdmissions block generates new agents at the rate defined by the AdmissionsPerDay dynamic variable. The arrivals are defined in the form of interarrival time and not in the form of rate, because the rate is not re-evaluated during the simulation, whereas the interarrival time is re-evaluated after each new agent.

If the value of the dynamic variable changes in between two subsequent event occurrences (or in between two agent arrivals), this will not be "noticed" immediately, but only at the next event occurrence (or next agent arrival).

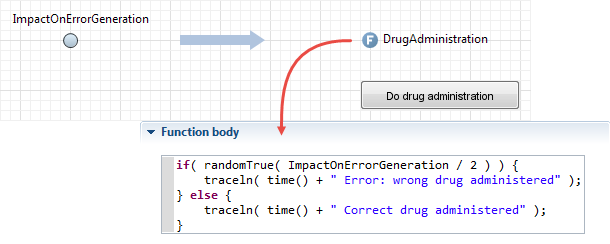
E. The SD variable is used in a decision made in the DE part of the model

This example shows that SD variables can be freely used in the actions and expressions inside the discrete elements of the model: conditions, functions, actions of events and transitions, On enter / On exit fields of flowchart blocks, and so on. Dynamic variables in that sense do not differ at all from variables.

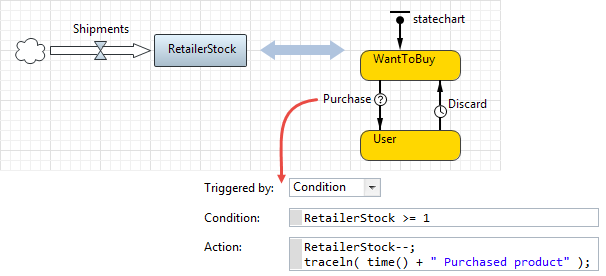
Discrete elements -> system dynamics

F. The SD stock triggers a statechart transition, which, in turn, modifies the stock value

Here, the interface between the SD and the statechart is implemented in the pair condition / action. In the WantToBuy state, the statechart tests if there are products in the retailer stock, and if there are, buys one and changes the state to User.

You can freely change the values of the system dynamics stocks from outside the system dynamics part of the model. This does not interfere with the differential equation solving: the integrator will start with the new value. However, trying to change the value of a flow or dynamic variable that has an equation associated with it, is not correct: the assigned value will be immediately overridden by the equation, so assignment will have no effect.

G. The size of the agent population is used in the SD equation

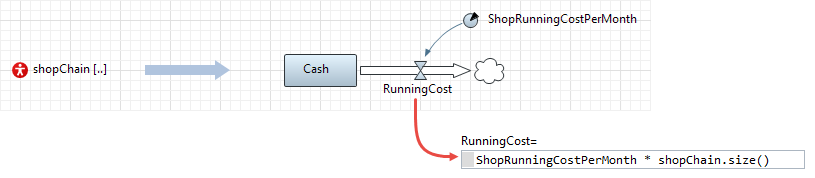
The equations in the system dynamics part of the model can reference not only the SD variables and functions, but also the arbitrary discrete elements in the model. The RunningCost flow out of the Cash stock depends on the current number of shops in the chain, and each shop is an agent. The call to the shopChain.size() function returns the number of agents in the shopChain population.

H. The statistics on agent population impacts an SD variable

This method may be inefficient!

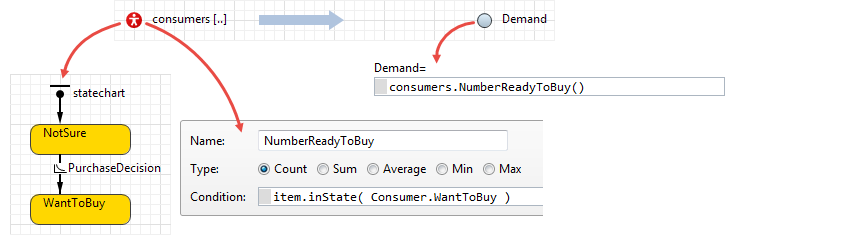
Here, we are calculating the number of agents in a population that are in a particular WantToBuy state, and provide that value to the Demand SD variable.

In this case this is implemented in a straightforward way: the call to the NumberReadyToBuy() is typed directly into the equation field of Demand, and, therefore, statistics are re-evaluated at each integration step. If there are many agents in the model, this may be very time consuming and slow down the simulation:

I. The statistics on agent population impacts an SD variable

This method is efficient.

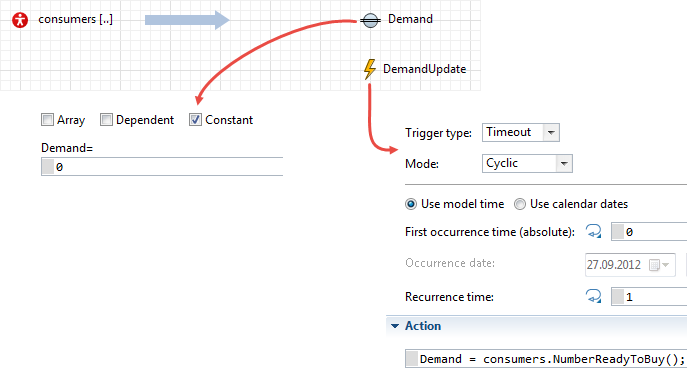
In this case the same functionality as in example H is implemented more efficiently: the Demand variable is declared as "constant" (the Constant checkbox is set), and its value is periodically updated by the DemandUpdate recurrent event, whose frequency is significantly lower than the frequency of the numeric integrator:

J. The SD variable is controlled by the statechart state

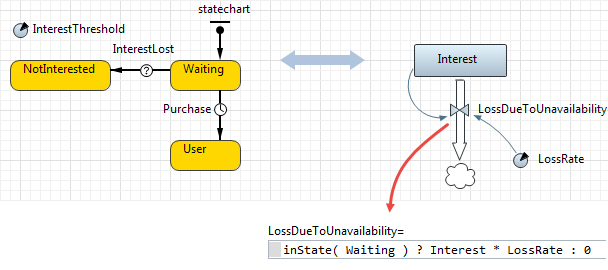
Consider a model of a consumer who has a certain degree of interest in the product modeled by an "individual" Interest SD stock (located inside the consumer model). As the consumer is waiting for the product to become available, his interest decreases. This is captured by the equation of the LossDueToUnavailability flow that contains the call to inState( Waiting ) function. This function returns true if the statechart is in a given state, and false otherwise. In this model you also can implement a loop back from the SD to the statechart if you let the InterestLost transition occur when the value of the stock falls below a certain threshold.

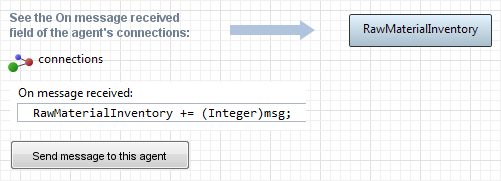
K. A message received by an agent modifies the internal SD stock

Such agent can be an element of a supply chain where orders and shipments are modeled as messages between agents. In this case the incoming message is of the Integer type (same as int) and is treated as the amount of raw material shipped to this agent. The internal dynamics of the agent are modeled in the system dynamics way, and the RawMaterialInventory stock is incremented upon the message arrival (see the On message received property of the agent's connections). In more complex models the message can include the supplier ID, the type of product, and so on.

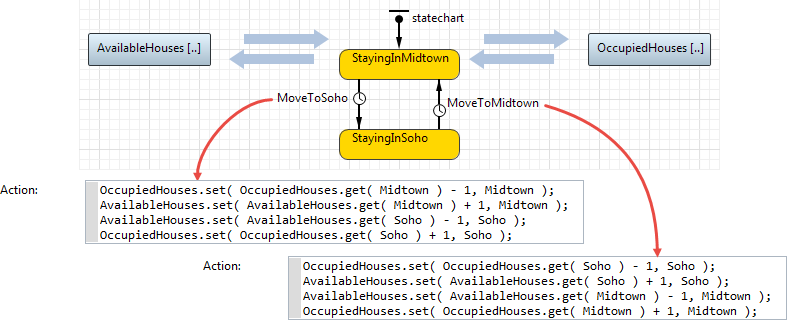
L. The bi-directional flow between the SD stocks is implemented outside the SD

The two stocks model available and occupied houses in the two neighborhoods of NYC. Both stocks are arrays with the {Midtown, Soho} dimension. People (agents) may move from Midtown to Soho and vice versa. When leaving, they decrement the bucket of the Occupied stock and increment the bucket of the Available stock. Then they do the reverse operation on the pair of buckets belonging to their new location.

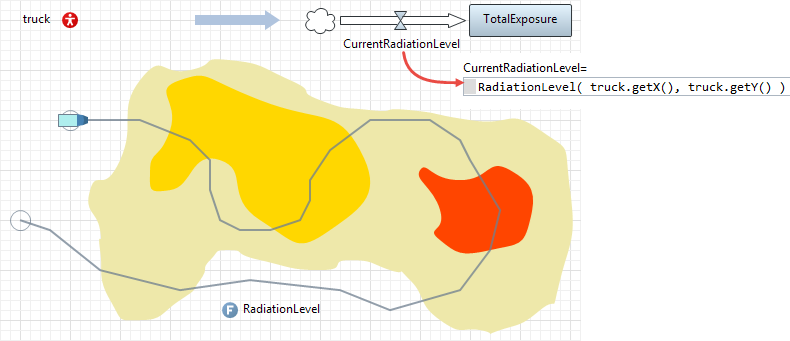
M. The SD stock accumulates the "history" of the agent motion

This is an interesting example of the cooperation between the system dynamics and agent-based modeling. The value of the TotalExposure stock is constantly updated as the mobile agent moves through the area contaminated by radiation. The value of the incoming CurrentRadiationLevel flow is set to the radiation level at the coordinates of the truck agent. As the truck moves or stays, the stock receives and accumulates a dose of radiation per time unit. Again, in the SD equation, we are referencing the agent and calling its function.

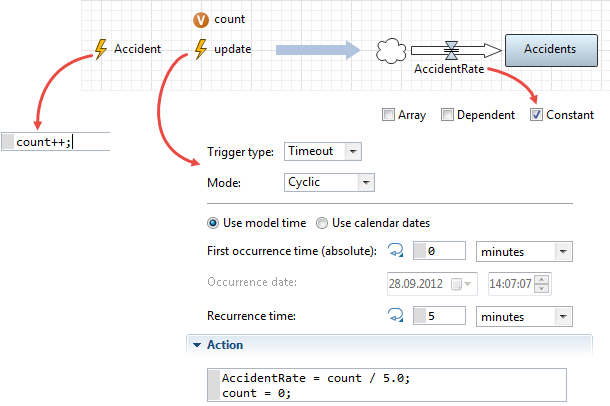
N. Measuring discrete event rate and feeding it to the SD flow

This method is not recommended.

Suppose you want to create an SD reflection of the discrete event flow. The discrete events may model things like purchases, arrivals, accidents, decisions, and so on. The technique described in this case can be used, but it is not recommended. The technique works as follows: the auxiliary update recurring event counts the number of Accident occurrences with a fixed interval, and sets AccidentRate to the number divided by the interval duration. This is, in fact, a rough derivative calculation. This implementation requires two auxiliary elements and the correct choice of the update interval.

Whenever possible, we recommend to directly update the stock, and not the flow. In this case, the original Accident event could increment the Accidents stock on each occurrence. This will be a 100% accurate solution without any unnatural constructs.

O. Referencing DE objects in the SD formula

In this example, the ProductionRate flow switches between 0 and 1, depending on whether the finished products inventory (the number of agents in the FinishedGoods queue returned by the size() function) is greater than 2 or not. Again, one can close the loop by letting the SD part control the production process.

Agent based <-> discrete event

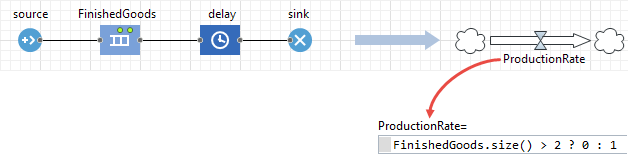
P. A server in the DE process model is implemented as an agent

Imagine complex equipment, such as a robot or a system of bridge cranes. The behavior of such objects is often best modeled "in agent based terms" by using events and statecharts. If the equipment is a part of the manufacturing process being modeled, you need to build an interface between the process and the agent representing the equipment.

In this example, the statechart is a simplified equipment model. When the statechart comes to the Idle state, it checks if there are agents in the queue. If yes, it proceeds to the Working state and, when the work is finished, unblocks the Hold block, letting the agent exit the queue. The Hold block is set up to block itself again after the agent passes through.

The next agent will arrive when the equipment is in the Idle state. To notify the statechart, we call the function onChange() upon each agent arrival (see the On enter action of the queue).

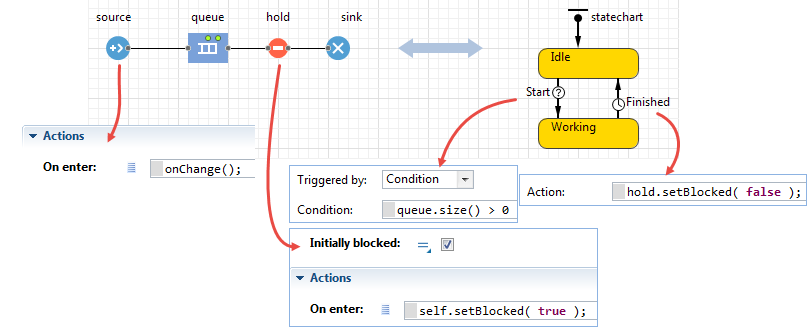
Unlike the models with continuously changing SD elements, pure DE models (with conditionally triggered events and transitions) do not monitor conditions continuously. The event's condition is evaluated when the event is reset. The transition's condition is evaluated when the statechart comes into the transition's source state. And then the conditions are re-evaluated when something happens to the agent where they are located, or when its onChange() function is called.

Q. The agent removes agents from the DE queue

Here, the supply chain is modeled using discrete event constructs; in particular, its end element, the retailer stock, is a Queue block. The consumers are outside the discrete event part, and they are modeled as agents. Whenever a consumer comes to the WantToBuy state, it checks the RetailerStock and, if it is not empty, removes one product unit. Again, as this is a purely discrete model, we need to ensure that the consumers who are waiting for the product are notified about its arrival – that's why the onChange() code is placed in the On enter action of the RetailerStock queue.

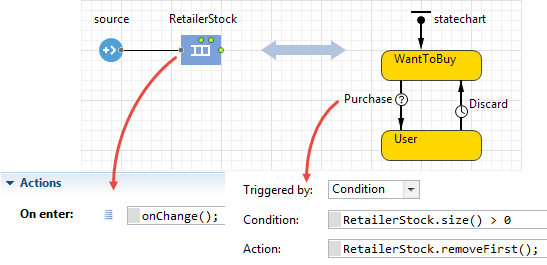
In this simplified version, there is only one consumer whose statechart is located on the same canvas as the supply chain flowchart. In the full version there would be multiple agents-consumers and, instead of calling onChange(), the retailer stock would notify every consumer in a loop, see example R.

R. The incoming message injects agents into the DE process

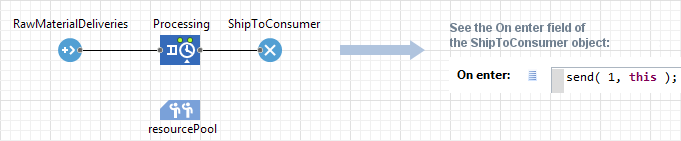
In the following two examples the process flowcharts are put inside agents. This architecture can be used in supply chain models. The message received by the agent has a meaning of raw material shipment that starts the manufacturing process. In the On message received action the agent injects agents into the flowchart by calling the inject() Source block function. The RawMaterialDeliveries block works in the manual" mode: it does not generate agents unless inject() is called.

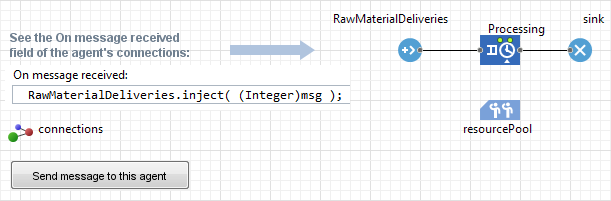
S. A process inside the agent initiates an outgoing message

In this case the manufacturing process ends with the ShipToConsumer Sink block. When an agent representing the finished product unit gets there, before it disappears from the process, the Sink sends out the message using the send() agent interface function.

In this simplified model, the message is just an integer number 1. In more realistic cases, you can send out the agent itself or batches of multiple agents. On the receiving end, the agents can be directly injected into the process. The Exit — Enter pair should be used then, instead of the Sink — Source pair.

How can we improve this article?