Функция распределения масс
Распределение
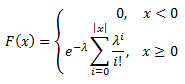
Мат. ожидание
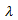
Дисперсия

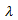
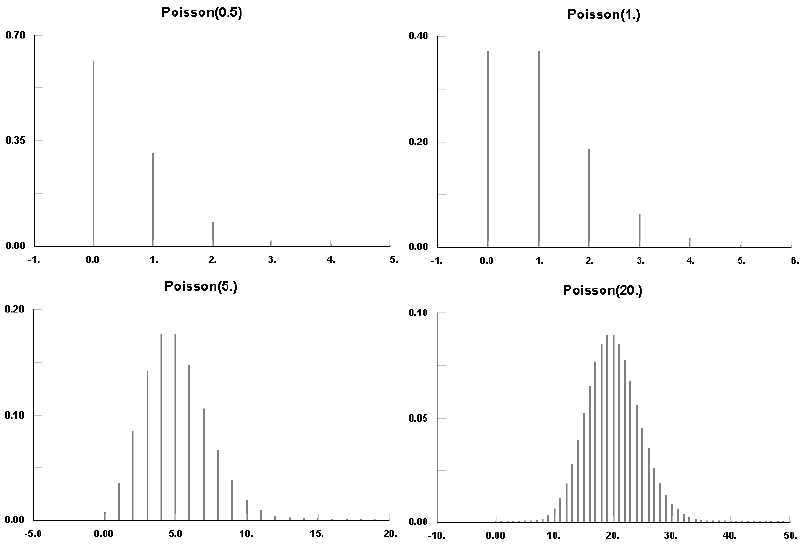
Распределение Пуассона — это дискретное распределение, ограниченное снизу нулем и не ограниченное сверху. Распределение Пуассона является предельным случаем гипергеометрического распределения.

Частое применение распределения Пуассона обусловлено тем, что оно описывает возникновение редких событий с неизменной частотой, К такому типу относятся многие события в пространстве и во времени, такие как инициирование телефонных вызовов, возникновение дефектов в полупроводниковом производстве, а также выявление любых иных дефектов в процессе контроля качества, распределение молекул и звезд, географическое распространение растений, дробовой шум т.д. Оно служит важной отправной точкой в теории очередей и теории надежности. Следует отметить, что время между возникновениями (дефектами) распределяется по экспоненциальному закону, поэтому такое распределение удобно в частности использовать на начальных этапах изучения даже более сложных процессов. Максимум распределения Пуассона приходится на область около lambda, при удалении в обе стороны оно быстро спадает.

Генерирует значение согласно распределению Пуассона.

Имя	Тип	Описание
lambda	double	частота возникновения

Тип	Описание
int	сгенерированное значение

Генерирует значение согласно распределению Пуассона с помощью заданного генератора случайных чисел.

Имя	Тип	Описание
lambda	double	частота возникновения
r	java.util.Random	генератор случайных чисел

Тип	Описание
int	сгенерированное значение

Эта статья содержит материалы из документа Stat::Fit User’s Manual. © 2016 Geer Mountain Software Corp. Все права сохранены.

Как мы можем улучшить эту статью?

Отправить