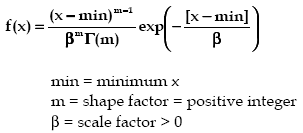
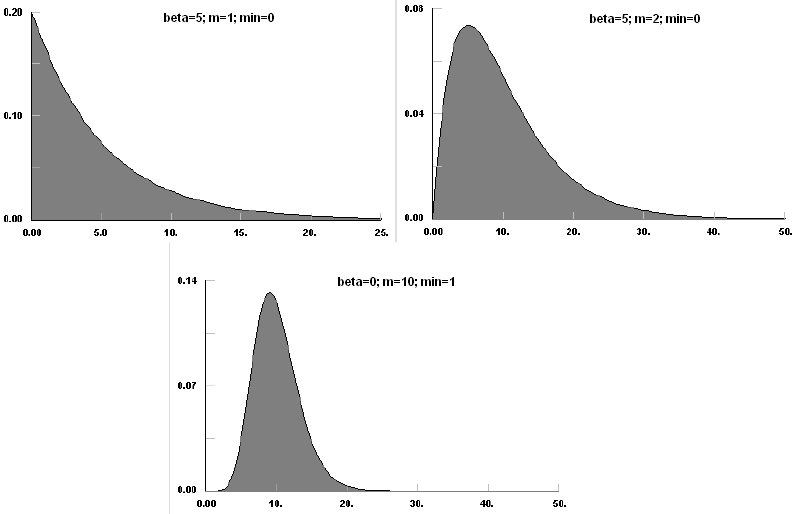
Распределение Эрланга является непрерывным распределением, ограниченным снизу. Оно представляет собой особый случай Гамма распределения, где параметр m может принимать только положительные целые значения. По существу, у распределения Эрланга нет области, в которой F(x) стремится к бесконечности при минимальном значении x [m<1], но при m=1 у него есть особый случай, при котором оно сводится к экспоненциальному распределению.
Распределение Эрланга широко используется в теории надежности и теории массового обслуживания, а следовательно и в дискретно-событийном моделировании, поскольку оно может рассматриваться как сумма m экспоненциально распределенных случайных переменных, каждая со своим средним beta.
Генерирует значение согласно распределению Эрланга.
| Имя | Тип | Описание |
|---|---|---|
| beta | double | параметр масштаба > 0 |
| m | int | параметр формы (положительное целое) |
| min | double | минимальное значение x |
| Тип | Описание |
|---|---|
| double | сгенерированное значение |
Генерирует значение согласно распределению Эрланга с параметром min=0. Эквивалентно erlang(beta, m, 0).
| Имя | Тип | Описание |
|---|---|---|
| beta | double | параметр масштаба > 0 |
| m | int | параметр формы (положительное целое) |
| Тип | Описание |
|---|---|
| double | сгенерированное значение |
Генерирует значение согласно распределению Эрланга с помощью заданного генератора случайных чисел.
| Имя | Тип | Описание |
|---|---|---|
| beta | double | параметр масштаба > 0 |
| m | int | параметр формы (положительное целое) |
| min | double | минимальное значение x |
| r | java.util.Random | генератор случайных чисел |
| Тип | Описание |
|---|---|
| double | сгенерированное значение |
Эта статья содержит материалы из документа Stat::Fit User's Manual. © 2016 Geer Mountain Software Corp. Все права сохранены.
-
Как мы можем улучшить эту статью?
-

