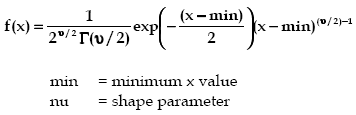
The chi-squared distribution is a continuous distribution bounded on the lower side. Note that the chi-squared distribution is a subset of the Gamma distribution with beta = 2 and alpha = nν/2. Like the Gamma distribution, it has three distinct regions. For nν = 2, the chi-squared distribution reduces to the exponential distribution, starting from a finite value at minimum x and decreasing monotonically as x increases. For nν < 2, the chi-squared distribution tends to infinity at minimum x and decreases monotonically for increasing x. For nν > 2, the chi-squared distribution is 0 at minimum x, peaks at a value that depends on nν, decreasing monotonically thereafter.
Because the chi-squared distribution has no scaling parameter, its use is somewhat limited. Frequently, this distribution attempts to represent data with a clustered distribution with nν less than 2. However, it can be viewed as the distribution of the sum of squares of independent unit normal variables with nν degrees of freedom and is used in many statistical tests.
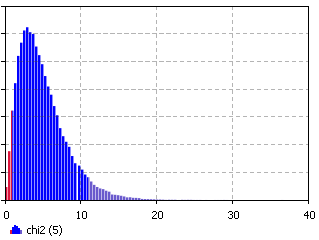
Examples of each of the regions of the chi-squared distribution are shown above. Note that the peak of the distribution moves away from the minimum value for increasing ν, but with a much broader distribution.
- Description
- Generates a sample of the chi-squared distribution.
- Parameters
-
Name Type of value Description nu double The shape parameter. min double The minimum x value. - Result
-
Type Description double The generated sample.
- Description
- Generates a sample of the chi-squared distribution with min set to 0. Is equivalent to chi2(nu, 0).
- Parameters
-
Name Type of value Description nu double The shape parameter. - Result
-
Type Description double The generated sample.
- Description
- Generates a sample of the chi-squared distribution using the specified random number generator.
- Parameters
-
Name Type of value Description nu double The shape parameter. min double The minimum x value. r java.util.Random The random number generator. - Result
-
Type Description double The generated sample.
This document includes content from the “Stat::Fit User’s Manual”. Copyright 2016 Geer Mountain Software Corp.
-
How can we improve this article?
-


